SPECTROSCOPIE - Spectrographes et spectromètres optiques

SPECTROSCOPIE - Spectrographes et spectromètres optiques

Les spectrographes et les spectromètres optiques sont des instruments permettant d’analyser la répartition spectrale de l’énergie dans une onde électromagnétique. Dans ce contexte sont considérés comme optiques des rayonnements dont la longueur d’onde est comprise entre 5 nm pour l’ultraviolet lointain et 300 猪m pour l’infrarouge lointain. Pour les longueurs d’onde plus grandes, on utilise les techniques des guides et des cavités ^{[cf. HYPERFRÉQUENCES]} et, pour les longueurs d’onde plus courtes, les techniques des rayons X (cf. rayons X) et des rayonnements ionisants. Les instruments spécialisés pour les radiations ultraviolettes sont décrits dans l’article ULTRAVIOLET.

Les spectrographes enregistrent les spectres sur plaque photographique, leur domaine d’application est limité aux radiations dont la longueur d’onde est inférieure à 1 猪m. Ces instruments restés longtemps outils de prédilection des astronomes sont aujourd’hui remplacés par des spectromètres multicanaux qui utilisent des matrices de photodiodes.

Les spectromètres enregistrent les spectres élément par élément à l’aide d’un détecteur photoélectrique suivi d’une chaîne de mesure appropriée. Les détecteurs employés sont très variés: photomultiplicateur, photodiode, photopile, cellule photorésistante, phototransistor, bolomètre, etc.

Les spectromètres multicanaux permettent l’enregistrement simultané des éléments d’un spectre grâce à l’utilisation de détecteurs multicanaux tels que les barrettes et les matrices de photodiodes. Ces instruments, souvent couplés à des systèmes informatiques d’acquisition, de traitement et de stockage des données, connaissent un développement rapide.

Les spectrophotomètres mesurent surtout les flux dans des bandes spectrales généralement moins étroitement définies. Les spectrophotomètres d’absorption donnent les variations spectrales du rapport du flux transmis par un échantillon au flux incident ^{[cf. SPECTROPHOTOMÉTRIE]}.

Les monochromateurs ne sont munis d’aucun récepteur. Ils transmettent une bande spectrale de largeur déterminée vers un autre instrument.

La qualité fondamentale d’un appareil spectroscopique est son aptitude à distinguer deux radiations dont l’écart de longueur d’onde 嗀凞 est petit devant la longueur d’onde . On appelle pouvoir de résolution ou résolvance le rapport R = / 嗀凞 correspondant à la plus petite valeur de 嗀凞 , appelée limite de résolution. Les pouvoirs de résolution des instruments spectroscopiques vont de quelques centaines pour les plus simples à plusieurs millions pour certains montages interférentiels.

Les spectres optiques que l’on obtient grâce à ces instruments sont un outil puissant pour connaître la structure électronique des atomes et des molécules. La haute résolution fournit même avec les structures hyperfines des données sur la structure des noyaux atomiques. Ces spectres permettent aussi l’étude de sources hors de notre portée (astrophysique, hautes températures, plasmas), l’analyse minérale ou organique. La majeure partie des connaissances actuelles de l’Univers a pour origine l’étude d’un spectre (analyse et synthèse de la lumière blanche par Newton, théorie des quanta de Planck, théorie atomique de Bohr, mécanique quantique de De Broglie et ses successeurs, atmosphères planétaires et stellaires, expansion de l’Univers). Les analyses chimiques des contrôles de processus industriels, les analyses biomédicales, les analyses de pollutions atmosphériques sont pour une grande part faites par spectrométrie optique.

Les méthodes et les appareils destinés à analyser les spectres optiques sont très variés. Certains sont plus résolvants, d’autres plus rapides, certains plus sensibles ou plus simples d’emploi. Seule une estimation complète des avantages et des inconvénients d’une méthode ou d’un instrument permet de faire un choix judicieux, et ce choix reste spécifique.

1. Caractéristiques générales d’un instrument

Fonction d’appareil

Lorsqu’un spectromètre est éclairé par une radiation monochromatique (par exemple, la lumière émise par un laser ou, plus généralement, toute radiation dont le spectre est beaucoup plus fin que ce que peut résoudre l’instrument), sa réponse n’est pas parfaitement monochromatique, mais s’étend sur un domaine spectral que l’on peut caractériser par sa largeur à mi-hauteur. Cette largeur, mesurée en unités spectroscopiques (longueur d’onde ou nombre d’ondes 靖 = 1/ ), est, par définition, la limite de résolution 嗀凞 ou 嗀靖 de l’instrument. En première approximation, la forme de la courbe ainsi enregistrée ne dépend pas de la longueur d’onde de la lumière incidente, ni de l’intensité de la source. C’est une caractéristique de l’instrument appelée sa fonction d’appareil A ( ). On montre dans ces conditions que si le spectromètre est éclairé par une distribution spectrale quelconque de puissance 煉S ( )/ 煉 , sa réponse S ( ) est le produit de convolution de 煉S ( )/ 煉 par A ( ):

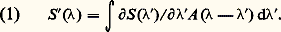La réponse S ( ) est identique à 煉S ( )/ 煉 si la fonction d’appareil A ( ) est assimilable à une distribution de Dirac, qui est l’unité du produit de convolution. C’est vers cette limite que tendent les fonctions d’appareil très fines des instruments les plus résolvants.

Pouvoir de résolution théorique

La limite de résolution dépend en général de paramètres sur lesquels l’utilisateur d’un instrument peut agir, comme la largeur des fentes. Mais, pour un instrument donné, il existe une limitation fondamentale due à la nature même de l’onde lumineuse, qui impose une limite supérieure R ⁰ au pouvoir de résolution R , limite appelée pouvoir de résolution théorique. Dans les instruments à fentes et disperseur, le pouvoir de résolution théorique n’est qu’une limite dont on ne peut s’approcher qu’au prix d’une grande perte de lumière. Dans les instruments interférométriques, au contraire, le pouvoir de résolution effectif est égal ou à peine inférieur au pouvoir de résolution théorique.

Bien que l’on distingue en spectrométrie les instruments classiques (appareils à fentes et disperseurs) des instruments interférentiels, tout appareil d’optique est interférentiel en ce sens que la formation d’une image est une interférence constructive entre des rayons issus d’un même point objet. Il en résulte une limitation commune à tous les instruments d’analyse spectrale, qui fixe la valeur du pouvoir de résolution théorique à partir d’un paramètre fondamental caractérisant un instrument donné: la plus grande différence de chemin optique D ^m entre deux rayons ayant traversé l’instrument. Le chemin optique, qui est le chemin géométrique multiplié par l’indice de réfraction du milieu traversé, tient compte du ralentissement de la lumière dans ce milieu.

Une radiation de longueur d’onde donnera donc en sortie une image avec un ordre d’interférence k = D ^m/ = 靖D ^m. Le principe de la séparation de deux longueurs d’onde voisines et 梁 嗀凞 est une généralisation à l’espace du principe d’incertitude temps fréquence 嗀f T 年 1. De même que sur une durée T on distinguera deux fréquences différentes de 1/T , de même sur une différence de chemin optique D ^m on distinguera deux nombres d’ondes différents de 嗀靖 = 1/D ^m, correspondant à une variation 嗀k = D ^m 嗀靖 de l’ordre d’interférence égale à 梁 1. Ce qui distingue la spectrométrie des longueurs d’onde optiques de celle des fréquences, c’est que la différence de chemin optique D ^m est variable avec la longueur d’onde , ce qui complique l’écriture de la variation 嗀k :

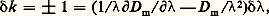d’où:

où l’on prend la valeur absolue parce que R ⁰ est par définition positif.

Luminosité

La valeur du pouvoir de résolution théorique n’est pas le seul critère à prendre en compte pour caractériser un spectromètre. Le flux qu’il est capable de transmettre au détecteur, pour une source de luminance donnée, est lié à l’étendue géométrique U du faisceau qu’il peut accepter et à son facteur de transmission, qui définissent sa luminosité. L’étendue du faisceau acceptable par un spectromètre est en général faible, et est donnée par le produit de la surface de la pupille S (section droite du disperseur ou surface des miroirs d’un interféromètre) par l’angle solide 行 sous-tendu à l’infini par les fentes d’un spectromètre à disperseur ou par le diaphragme isolant le centre des anneaux à l’infini d’un interféromètre:

L’étude des différents instruments montre que le produit de l’étendue de faisceau disponible par le pouvoir de résolution U 憐 R est un invariant caractéristique d’un instrument et d’une technique.

2. Spectromètres à fentes et disperseur

L’architecture d’un spectromètre à fentes utilisant un disperseur (prisme ou réseau ou association des deux) est donnée par la figure 1: la fente d’entrée est située dans le plan focal d’un collimateur et sélectionne les rayons parallèles à un même plan. Après dispersion, ces rayons se retrouvent en première approximation parallèles à des plans dont la direction dépend de la longueur d’onde de la radiation incidente. C’est par une fente de sortie, conjuguée de la fente d’entrée dans le plan focal de l’objectif de sortie, que l’on fait la sélection de ces longueurs d’onde dans le cas d’un monochromateur ou d’un spectromètre à balayage. On placera dans le plan focal de sortie une émulsion photographique ou un détecteur multicanal dans le cas d’un spectrographe ou d’un spectromètre multicanal. On montre très simplement que la largeur angulaire 嗀i ¹ de la fente d’entrée doit être adaptée à la largeur angulaire 嗀i ² de la fente de sortie ou à la limite de résolution angulaire du détecteur multicanal. La largeur angulaire de fente la plus petite acceptable est déterminée par la largeur angulaire de la tache de diffraction de la pupille du disperseur. Si la pupille est un rectangle de largeur L , la plus petite largeur angulaire qui définira le pouvoir de résolution théorique R ⁰ est /L . Cette largeur devient 1,22 /D dans le cas d’une pupille circulaire de diamètre D .

La limite de résolution spectrale 嗀凞 est déterminée par la largeur angulaire 嗀i ² de la fente de sortie et la dispersion angulaire D ² = 煉i ²/ 煉 :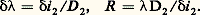

Le flux transmis pour une luminance de source donnée est proportionnel à 嗀i ². Le pouvoir de résolution est proportionnel à son inverse. Le produit étendue de faisceau 憐 pouvoir de résolution est donc un invariant caractéristique d’un instrument donné.

Le pouvoir de résolution théorique s’exprime simplement en fonction des largeurs de pupille d’entrée ou de sortie et des dispersions angulaires correspondantes:

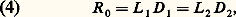et le produit de l’étendue de faisceau U par le pouvoir de résolution R s’écrit:

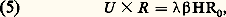où 廓 est la hauteur angulaire de la fente et H la hauteur de la pupille. Ce produit est d’autant plus grand que les dimensions du spectromètre sont grandes et que le pouvoir de résolution théorique R ⁰, lui-même relié à la largeur L de la pupille, est grand.

Spectromètres à prisme

La différence de chemin optique entre un rayon qui passe par l’arête d’un prisme et un rayon qui passe par sa base est nulle. La dispersion angulaire ne vient que de la variation de l’indice en fonction de la longueur d’onde. L’expression du pouvoir de résolution théorique du prisme déduite de la relation 2 est:

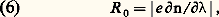ce qui conduit à des pouvoirs de résolution de l’ordre de quelques milliers pour des prismes de 10 centimètres d’épaisseur à la base. L’étendue de faisceau, donc la luminosité d’un prisme pour une source de luminance donnée, est liée à R par la valeur de ce pouvoir de résolution théorique.

Les montages pratiques sont très divers. Dans le montage autocollimateur de Littrow (fig. 2), le même composant sert de collimateur d’entrée et d’objectif de sortie, le prisme travaillant en réflexion ou en double passage par transmission avec réflexion sur un miroir plan. Fente d’entrée et fente de sortie ou détecteur se trouvent alors juxtaposés dans un même plan.

Dans les petits spectroscopes de poche à vision directe (fig. 3), trois prismes sont accolés dont l’un placé tête-bêche compense la déviation des deux autres, mais pas leur dispersion. C’est le montage d’Amici. Avec un encombrement total qui n’excède par une quinzaine de centimètres, ils permettent d’observer le spectre visible avec un pouvoir de résolution de l’ordre de 1 000, tout juste suffisant pour séparer les deux composantes de structure fine de la raie de résonance du sodium.

Le prisme est le premier disperseur appliqué à l’analyse spectrale en 1666 par Isaac Newton. De bonne transparence et facile d’emploi, ce disperseur est néanmoins limité aux pouvoirs de résolution inférieurs à quelques milliers et n’est plus guère employé que comme séparateur d’ordres en association avec le réseau. Sa grande transparence et le fait qu’il n’est pas soumis au phénomène de superposition d’ordres comme les réseaux et les autres spectromètres interférentiels justifient néanmoins son emploi dans certains montages. La mise en série de trois ou quatre prismes (fig. 4), en ajoutant leurs dispersions, permet d’augmenter la résolution, mais le flux transmis est atténué aux extrémités du spectre où se manifeste un silhouettage pupillaire important.

Le prisme de Pellin et Broca (fig. 5) comportant une réflexion interne permet de conserver la symétrie entrée-sortie par seule rotation du prisme en gardant les fentes d’entrée et de sortie fixes sur deux bras perpendiculaires. Dans les spectromètres modernes, en particulier les spectromètres astronomiques, l’association d’un prisme et d’un réseau permet d’annuler la déviation du faisceau, comme dans le montage d’Amici, avec le prisme de Carpenter aussi appelé grism , par contraction de grating et de prism (fig. 6). Bien que les déviations se compensent, les dispersions du prisme et du réseau s’ajoutent dans ce montage.

Des instruments destinés à l’infrarouge ou à l’ultraviolet ont été construits avec des prismes taillés dans des cristaux d’halogénures alcalins. Délicats à usiner, ces matériaux sont fragiles, parfois hygroscopiques.

Pour accroître les pouvoirs de résolution accessibles aux prismes, on a aussi utilisé des prismes à liquides. André Couder a construit des disperseurs en immergeant jusqu’à sept prismes dans un ester réfringent. Un prisme à liquide a longtemps été le disperseur placé au fond du puits de 10 mètres du spectromètre placé verticalement sous le grand électroaimant de Bellevue (fig. 7). Sa section droite de 30 centimètres de largeur n’avait comme seuls défauts que les hétérogénéités liées aux turbulences thermiques au sein du liquide. À cette échelle, les turbulences de l’atmosphère sont tout aussi redoutables, et il fallait que personne ne soit descendu dans le puits pendant plus de douze heures pour pouvoir faire un enregistrement à longue pose avec ce spectromètre.

La mesure des longueurs d’onde dans un spectromètre à prisme nécessite un étalonnage de l’instrument avec un grand nombre de radiations de référence, parce que la dispersion 煉n / 煉 n’est pas modélisable simplement. Le spectre du fer a longtemps servi pour un tel étalonnage de la dispersion des instruments spectrométriques.

Spectromètres à réseau

Le réseau est de beaucoup le disperseur le plus utilisé dans les spectromètres pour les domaines visible, infrarouge et ultraviolet. Les constructeurs proposent toute une gamme d’instruments dont les distances focales vont de 100 millimètres à quelques mètres, permettant d’atteindre des pouvoirs de résolution allant de quelques dizaines de milliers à quelques centaines de milliers. On trouve des montages de laboratoire pour lesquels le spectromètre est construit in situ, comme c’était le cas du spectromètre de 10 mètres de distance focale du grand électroaimant des laboratoires Bellevue, et permettant d’atteindre des pouvoirs de résolution de l’ordre de 50 000 avec un prisme à liquide et de plus de 1 million avec un réseau.

Le pouvoir de résolution théorique du réseau est donné par la différence de marche maximale entre rayons extrêmes. Si le réseau travaille dans l’ordre k , ce qui signifie que la différence de marche entre deux rayons diffractés par deux traits consécutifs est égale à k longueurs d’onde:

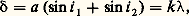la différence de marche maximale est égale à Nk , où N est le nombre total de traits du réseau, d’où, si L = Na est la largeur du réseau, on déduit le pouvoir de résolution théorique de la relation 2:

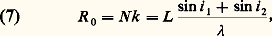k est de l’ordre de quelques unités à quelques dizaines et N va de quelques dizaines de milliers à quelques centaines de milliers. Le pouvoir de résolution théorique d’un réseau va de quelques milliers à près d’un million. Les instruments commerciaux ont généralement un pouvoir de résolution inférieur à 100 000, mais certains atteignent des pouvoirs de résolution de quelques centaines de mille avec des encombrements de 2 à 3 mètres. Le montage le plus répandu est le montage dit de Ebert (fig. 8) pour lequel un grand miroir sphérique (ou deux miroirs plus petits ayant le même centre) travaille comme collimateur d’entrée et comme objectif de sortie, dans une configuration symétrique qui annule les aberrations impaires telle que la coma (cf. OPTIQUE - Images optiques). L’astigmatisme, qui n’est pas compensé, est corrigé par l’emploi de fentes courbes à l’entrée et à la sortie, appelées fentes de Fastie, de telle sorte que la focale tangentielle d’un point de la fente d’entrée reste toujours parallèle à la zone correspondante de la fente de sortie (fig. 9).

Le problème des aberrations, dans le cas des spectrographes et des spectromètres multicanaux, est compliqué par la nécessité d’obtenir de bonnes images dans un champ étendu. Pour une utilisation optimale des détecteurs, on est conduit à former ces images avec des faisceaux aussi largement ouverts que possible. On doit donc recourir à des objectifs de courte distance focale et de grand rapport d’ouverture pour lesquels les aberrations géométriques sont encore plus critiques. Certaines chambres spectrographiques utilisent des lames de Schmidt, des châssis incurvés pour émulsions à support souple (fig. 10) ou des aplanisseurs de champ pour détecteur plan. Parfois, la surface sensible est immergée dans un liquide assurant une continuité d’indice avec une dernière lame correctrice.

La mesure des longueurs d’onde avec un réseau est facile et très exacte, parce qu’elle se fait en comparant les angles d’émergence avec l’angle d’émergence d’une radiation de référence, qui donne une mesure absolue du pas a du réseau. La superposition de différents ordres dans une même direction, qui est un inconvénient du réseau nécessitant l’isolation d’un intervalle spectral libre par un prémonochromateur, devient un avantage pour comparer les directions voisines de radiations de longueurs d’onde très différentes. La comparaison des longueurs d’onde lumineuses avec un réseau est exclusivement géométrique, ce qui justifie la très grande exactitude obtenue par Fraunhofer dans la comparaison qu’il a faite au milieu du siècle dernier entre les longueurs d’onde du spectre solaire.

Description de quelques instruments

Pendant de longues décennies, le spectrographe du foyer coudé du télescope de 1,93 m de diamètre de l’observatoire de Saint-Michel-de-Provence (fig. 11) fut un exemple de souplesse et d’adaptabilité à des problèmes très divers. Un réseau interchangeable pouvait être couplé à plusieurs chambres photographiques en fonction du problème traité. De grandes distances focales pour les objets brillants nécessitent l’accès à de grands pouvoirs de résolution, et des chambres très ouvertes pour l’étude des objets peu lumineux ne permettent que des pouvoirs de résolution plus faibles. Les quatre distances focales étaient égales à 2 mètres, 67 centimètres, 33 centimètres et 16,5 cm. Une dispersion de 7,6 nm/mm dans la chambre ouverte à f /1 conduit, avec une émulsion dont la limite de résolution est 20 猪m, à un pouvoir de résolution égal à 3 000 au centre du domaine visible, ce pouvoir passe à 125 000 pour la chambre la plus longue.

Les spectromètres astronomiques modernes ont vu leur architecture profondément remaniée par l’augmentation des diamètres de miroirs de télescopes (3,6 m pour les miroirs actuels, 10 m pour le Tek à miroirs multiples, 8 m pour le Very Large Telescope européen), par l’apparition des détecteurs matriciels photoélectriques qui remplacent les émulsions photographiques avec un bien meilleur rendement quantique, et qui étendent le domaine spectral vers l’infrarouge, et par l’utilisation des fibres optiques, associées ou non à des matrices de microlentilles, qui permettent d’adapter la géométrie des faisceaux à celle d’un spectromètre à fentes étroites et hautes. La hauteur d’une fente de spectromètre astronomique au foyer d’un grand télescope peut atteindre 400 millimètres pour une largeur de quelques dizaines ou quelques centaines de micromètres.

Ce sont, pour la plupart, des spectromètres à réseau en montage autocollimateur sous forte incidence (i⁰ de 50⁰ à 75⁰) associé à des chambres photographiques de distances focales et d’ouvertures variables au foyer desquelles on trouve des matrices de photodiodes 1 000 憐 1 000 pixels, 2 000 憐 2 000 pixels, et bientôt 4 000 憐 4 000 pixels. Ces matrices sont, le plus souvent, refroidies et atteignent des performances remarquables dans leur capacité à intégrer les flux faibles sur de longues durées, avec un rendement quantique à peu près de cent à mille fois meilleur que les émulsions photographiques. Quelques instruments sont aussi prévus pour fonctionner avec la caméra électronique Lallemand, qui permet d’intégrer photon par photon sur toute une nuit.

Les réseaux des spectromètres modernes sont souvent des réseaux échelles, dont les traits sont larges devant la longueur d’onde des radiations étudiées, ce qui permet de leur donner un profil en marche d’escalier favorable à une bonne efficacité lumineuse dans la direction de réflexion spéculaire sur les traits, qui sont autant de miroirs étroits. C’est la direction du «blaze» qui donne à ces réseaux un maximum d’efficacité voisin de 80 p. 100, parfois plus. Comme le pas de ces réseaux est grand devant la longueur d’onde, ils travaillent par conséquent dans des ordres élevés, et on doit séparer ces ordres par un dispositif à dispersions croisées qui permet de superposer sur un même détecteur un grand nombre d’ordres. Certaines radiations qui sont dispersées dans deux ordres successifs apparaissent deux fois sur le détecteur, avec une efficacité lumineuse évidemment moins bonne (fig. 12).

Les appareils destinés à l’étude des spectres de diffusion Raman ont une structure particulière liée à la nature du problème posé: un spectre de diffusion Raman (cf. effet RAMAN) est un ensemble de radiations très peu intenses dont les longueurs d’onde sont très voisines de la longueur d’onde de la radiation incidente, en général une radiation laser, observée par diffusion Rayleigh, avec une intensité 10 000 à 10⁶ fois plus forte. C’est essentiellement le taux de lumière parasite qui caractérise les performances d’un spectromètre Raman. Ce taux est fortement atténué si l’on fait passer la lumière à analyser successivement à travers deux ou même trois monochromateurs dont les bandes passantes sont synchronisées. Ces spectromètres doubles ou triples permettent d’atteindre un taux de lumière diffusée si faible que celui-ci est déterminé par les premiers miroirs et non plus seulement par les réseaux. Les réseaux modernes gravés sur une machine contrôlée interférentiellement, et surtout les réseaux holographiques dont la géométrie des traits est parfaite, ont apporté des progrès décisifs dans ce domaine.

3. Spectromètres à modulation

Le défaut des spectromètres à fentes est la faible étendue de faisceau admissible par une fente étroite. La grande disproportion entre la hauteur et la largeur d’une fente de spectromètre rend les conjugaisons optiques difficiles entre les sources habituelles et les spectromètres à fentes.

Plutôt que de filtrer des radiations monochromatiques par des fentes étroites, on peut aussi moduler sélectivement un ou plusieurs éléments spectraux pour les isoler de l’ensemble du flux transmis par l’instrument. La modulation peut être interférentielle ou géométrique à l’aide de grilles. La détection synchrone, ou toute autre détection sélective en fréquence, permet d’isoler le signal modulé du fond continu. Ces techniques s’appliquent aux détecteurs infrarouges dont le bruit propre est beaucoup plus puissant que le bruit de photons du grand flux continu parasite reçu par le détecteur.

C’est sur un dispositif interférentiel que le principe de la modulation sélective a été appliqué pour la première fois par Pierre Connes en 1958. Le principe du spectromètre interférentiel à sélection par l’amplitude de la modulation (S.I.S.A.M.) est le suivant: on remplace les deux miroirs d’un interféromètre de Michelson par des réseaux dont les dispersions sont de sens opposés (fig. 13). L’interféromètre ne donne donc de franges à l’infini que pour la radiation dont la longueur d’onde est renvoyée par les réseaux en parfaite autocollimation. Une variation de la différence de marche dans l’interféromètre (translation d’un réseau ou, plus simplement, oscillation de la lame compensatrice) donne donc un signal de modulation interférentielle pour cette radiation exclusivement. On peut montrer que la sélectivité de la modulation correspond à un pouvoir de résolution égal à deux fois le pouvoir de résolution théorique R ⁰ d’un réseau.

Une autre technique a été développée par André Girard en 1963. Dans un spectromètre à réseau, on remplace la fente d’entrée par une grille, et la fente de sortie par l’image monochromatique de cette grille à travers le spectromètre. Le facteur de transmission moyen de la grille est 0,5. Le facteur de transmission moyen à travers la grille de sortie est 0,25 sur la surface commune aux deux grilles, sauf si les images de grilles coïncident à la définition des détails de structure des grilles près, auquel cas tout le flux transmis par la première grille est transmis par la seconde grille avec un facteur de transmission moyen égal à 0,5. Le flux transmis par ce spectromètre éclairé par une radiation monochromatique est donné par la figure 14. On élimine le flux latéral transmis par l’ensemble des éléments spectraux qui ne sont pas centrés en faisant osciller un élément du spectromètre sur la largeur du pic central. Ce type de spectromètre est utilisé dans certaines expériences embarquées en ballon ou en fusée pour l’étude de l’atmosphère. Il a paru plus simple d’emploi qu’un interféromètre, mais l’expérience a montré que, si on cherche à atteindre le pouvoir de résolution théorique d’un grand réseau avec un spectromètre à grille, les tolérances du montage mécanique et des systèmes optiques sont comparables à celles d’un montage interférométrique.

On a aussi, plus récemment, construit aux États-Unis d’Amérique des spectromètres dont la grille d’entrée est une représentation binaire d’une ligne d’une matrice d’Hadamard (fig. 15). Une grille de sortie permet, par translation, de donner successivement la représentation des autres lignes de la matrice qui s’en déduisent par une permutation circulaire des éléments. On enregistre ainsi un signal photoélectrique qui est le produit du vecteur représentant le spectre par la matrice représentée par la grille. Il suffit de multiplier le vecteur ainsi enregistré par la matrice inverse pour revenir aux éléments spectraux. Cette technique, dite spectrométrie d’Hadamard, du nom du mathématicien français qui a étudié ces matrices originales, augmente à la fois la luminosité du spectromètre (qui comporte plusieurs fentes à l’entrée et à la sortie) et la rapidité d’enregistrement du spectre, puisque plusieurs éléments spectraux sont enregistrés simultanément (codage multiplex).

Bien que très élégantes sur le plan fondamental, ces techniques n’ont connu que peu ou pas de développement industriel. La spectrométrie par transformation de Fourier décrite plus loin, qui est à la fois plus lumineuse et qui étend le multiplexage à des domaines spectraux très larges, a pris une place prédominante sur le marché de la spectrométrie instrumentale.

4. Fabrication des réseaux

Réseaux gravés

Un bon réseau doit remplir deux conditions: d’une part, son efficacité lumineuse, c’est-à-dire le rapport entre l’énergie diffractée dans un ordre déterminé à l’énergie incidente, doit être aussi élevée que possible et, d’autre part, la forme de la surface d’onde réfléchie ou transmise doit être limitée par la diffraction.

L’efficacité lumineuse dépend de la forme des sillons, qui doivent agir comme de petits miroirs et orienter la lumière incidente dans la direction des interférences constructives, appelée direction du «blaze». Cette forme est liée à celle du diamant qui grave les traits (fig. 16).

La forme de la surface d’onde dépend de la forme de la surface gravée, mais aussi de la position des traits sur cette surface.

Pour fabriquer un réseau, on grave d’abord une matrice, fine couche d’aluminium déposée sur un substrat en silice optiquement poli. Le diamant est taillé de manière à découper, repousser et polir le métal pour donner aux traits la forme requise. À chaque trait, la matrice avance d’une même longueur, qui est le pas du réseau. À raison d’un trait en quelques secondes, la gravure d’une matrice prend plusieurs jours. La matrice est ensuite utilisée pour faire des répliques à l’aide de résines polymérisables déposées sur un support en verre ou en silice, une fine couche d’or facilitant la séparation. Une matrice peut donner de quelques dizaines à quelques centaines de répliques. On fabrique des répliques de répliques pour obtenir de grandes quantités (plusieurs milliers) avec une qualité homogène.

Une machine à graver un réseau est un ensemble mécanique de très haute précision; elle doit travailler sans interruption pendant plusieurs jours dans d’excellentes conditions de stabilité thermique (quelques centièmes de degré). Sur les machines modernes, l’avancement de la matrice est contrôlé par un dispositif interférentiel. La constance du pas est ainsi garantie d’une extrémité à l’autre de la matrice, à condition que les variations de l’indice de l’air dues aux variations de la pression atmosphérique soient compensées.

Réseaux holographiques

Une parfaite disposition des traits est obtenue en enregistrant, sur une résine photosensible, les franges d’interférences rectilignes et équidistantes données par deux ondes planes monochromatiques cohérentes (fig. 17). Le pas du réseau ainsi enregistré peut être très fin (jusqu’à une fraction de micromètre), et l’équidistance est garantie sur des dimensions appréciables par le phénomène des interférences lumineuses. On réalise assez facilement par ce procédé des réseaux de grandes dimensions dont la qualité de la surface d’onde diffractée ne dépend que des surfaces d’onde disponibles pour l’enregistrement des franges. En immergeant la résine dans un milieu d’indice élevé, on a fabriqué des réseaux comportant jusqu’à six mille traits par millimètre qui peuvent servir à l’étude de rayonnements de courte longueur d’onde.

Une autre possibilité offerte par cette technique est l’enregistrement de franges courbes sur des surfaces sphériques ou même toriques (fig. 18). On peut ainsi calculer des réseaux aux propriétés focalisantes intéressantes (réseaux concaves sans astigmatisme, en particulier pour l’ultraviolet lointain, avec un montage en incidence rasante qui améliore l’efficacité lumineuse).

En ajustant les paramètres tels que la direction des ondes incidentes par rapport à la normale à la surface sensible, on peut influer sur la forme des sillons imprimés dans la résine, et s’approcher d’un effet de miroitement (blaze) qui concentre l’énergie diffractée dans un ordre préférentiel.

La régularité géométrique d’un réseau holographique confère à ce dernier un très faible taux de lumière diffusée. Un bon réseau holographique diffuse moins qu’un miroir, ce qui le rend particulièrement efficace dans des problèmes à grande dynamique comme la spectrométrie Raman.

5. Spectomètres interférentiels

Avec le S.I.S.A.M. décrit au chapitre 3, les spectromètres interférentiels sont essentiellement dérivés de l’interféromètre de Fabry et Perot, d’une part, et de l’interféromètre de Michelson, d’autre part.

Interféromètre de Fabry et Perot

Par le jeu de réflexions multiples, l’interféromètre de Fabry et Perot offre la possibilité d’atteindre des pouvoirs de résolution très élevés sous un encombrement très réduit. Le facteur de transmission de deux miroirs plans parallèles séparés par une épaisseur e , éclairés par un faisceau perpendiculaire aux miroirs dont les pouvoirs réflecteur et transmetteur sont R et T , est une fonction périodique du nombre d’ondes 靖 établie par George Biddell Airy dès 1860 (fig. 19):

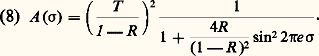Un faisceau de lumière monochromatique qui éclaire ces miroirs de manière isotrope donne des franges à l’infini sous forme d’une série d’anneaux fins. On peut photographier ces anneaux avec des radiations monochromatiques isolées (spectrographe), ou enregistrer la transmission sur l’axe en faisant varier e (spectromètre à balayage). Dans un cas comme dans l’autre, l’intervalle spectral libre est étroit:

et nécessite un spectre peu riche ou un prémonochromateur isolant une bande spectrale étroite.

Une caractéristique importante de l’étalon est sa finesse réflectrice:

qui représente le rapport de la largeur de l’intervalle spectral libre 靖 à la largeur spectrale à mi-hauteur 嗀靖 d’un pic de transmission. C’est aussi le nombre de réflexions efficaces que l’on peut observer entre les deux miroirs. On en déduit que la différence de marche maximale est égale à 2Ne et que le pouvoir de résolution théorique est: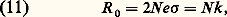

expression analogue à (7) obtenue pour le réseau, mais ici N , la finesse, qui représente le nombre de rayons efficaces, est de l’ordre de quelques dizaines, et k peut atteindre plusieurs dizaines ou plusieurs centaines de milliers. Une épaisseur de 2 centimètres, un pouvoir réflecteur égal à 90 p. 100 conduisent, pour une longueur d’onde égale à 0,5 猪m, à un pouvoir de résolution supérieur à un million.

La finesse réflectrice d’une cavité Fabry-Perot est d’autant meilleure que le pouvoir réflecteur des miroirs est proche de l’unité. Avec les couches multidiélectriques modernes, on sait atteindre des valeurs supérieures à 99 p. 100, correspondant à des finesses de plusieurs centaines, sur de larges domaines spectraux dans le visible et l’infrarouge. Dans l’ultraviolet, les pertes par diffusion sont plus sévères, et on peut tomber à des valeurs de l’ordre de 80 p. 100, conduisant à des finesses à peine supérieures à 10. Pour des cavités lasers devant travailler à longueur d’onde fixe, les progrès réalisés dans la fabrication de certaines couches sont remarquables: pour la fabrication des gyrolasers en particulier, des finesses de l’ordre de plusieurs dizaines ou centaines de milliers ont été obtenues. La finesse réflectrice n’est observée pratiquement que si le nombre de réflexions permises par le pouvoir réflecteur ne détériore pas la forme des surfaces d’onde. Le critère de lord Rayleigh, qui convient d’admettre des interférences conformes à la théorie avec des déformations des surfaces optiques inférieures à /4, réduit ici la tolérance à /4N . Il est donc très difficile d’observer de telles finesses dans de grandes étendues de faisceau.

L’avantage essentiel de l’interféromètre de Fabry et Perot, associé à la possibilité d’atteindre sous un encombrement réduit de grandes valeurs du pouvoir de résolution théorique, est le grand angle solide admissible défini par l’anneau central. Cet angle solide s’exprime très simplement en fonction de R ⁰:

et représente à peu près cent fois plus que l’angle solide accepté par la fente d’un spectromètre à réseau de même pouvoir de résolution. Associé au fait que l’étendue de faisceau présente la symétrie de révolution, cette grande luminosité est un atout exploité par les astronomes pour étudier la distribution des décalages par effet Doppler-Fizeau dans une nébuleuse, et obtenir ainsi des cartes de vitesses radiales. La première mesure de ce type avait été faite dès 1911 par Fabry et Buisson à l’observatoire de Marseille sur la nébuleuse d’Orion.

Filtres interférentiels

Les filtres interférentiels qui permettent de sélectionner des bandes spectrales beaucoup plus étroites que les verres colorés sont des étalons Fabry-Perot solides de faible épaisseur. Les deux couches multidiélectriques sont évaporées successivement sur un même substrat, avec interposition d’une couche transparente d’indice n dont l’épaisseur est déterminée en fonction de la longueur d’onde transmise et de la largeur de bande souhaitée. Des filtres colorés, dits filtres bloquants, absorbent les radiations transmises dans les autres ordres de l’interféromètre.

Bernard Lyot, astronome français, est connu dans le monde des opticiens pour avoir imaginé des filtres à partir d’un empilement de lames biréfringentes placées entre polariseur et analyseur. Les épaisseurs des lames étant en progression géométrique de raison 2, les différents spectres cannelés transmis ne coïncident que pour les radiations transmises par la lame la plus mince. Ces filtres sont caractérisés par une finesse égale à 2^N , où N est le nombre des lames, tout à fait comparable à celle d’un Fabry-Perot (fig. 20).

Tous ces filtres interférentiels sont sensibles à la température et à la direction d’incidence des rayons. C’est en jouant sur l’un ou l’autre de ces paramètres que l’on peut, dans une certaine mesure, ajuster avec grande précision la longueur d’onde de la radiation transmise par un filtre dont la bande passante est très étroite.

Étalons sphériques de Fabry-Perot

Lorsque l’épaisseur d’un étalon Fabry-Perot augmente, le pouvoir de résolution théorique de l’étalon augmente, et l’angle solide des anneaux à l’infini qui se resserrent diminue. Pour éviter que cet angle solide ne devienne inférieur à celui de la tache de diffraction des miroirs (étendue de faisceau inférieure à l’étendue élémentaire d’un mode de la cavité) et pour que les réglages géométriques ne deviennent trop critiques, P. Connes a inventé en 1958 le Fabry-Perot sphérique ou Fabry-Perot confocal. C’est un interféromètre formé de deux miroirs sphériques concaves dont le centre de l’un se trouve sur le sommet de l’autre, les deux foyers étant confondus (fig. 21).

Le fait que les rayons issus d’un même rayon incident et réfléchis par les miroirs quittent la cavité en étant confondus, et pas seulement parallèles, garantit une stabilité de l’ordre d’interférence quand on fait varier l’incidence. L’étendue de faisceau disponible s’en trouve augmentée. Dans un Fabry-Perot plan, seuls les rayons perpendiculaires aux miroirs ont cette propriété, ce qui justifie le fait que l’ordre d’interférence des anneaux à l’infini est stationnaire au centre des anneaux.

Les cavités des lasers de grande épaisseur ont toujours au moins un miroir sphérique, ce qui leur permet de fonctionner dans un seul mode spatial stable.

Spectrométrie par transformation de Fourier

Proposée en France par Pierre Jacquinot dès 1954 et simultanément en Grande-Bretagne par Peter B. Fellgett, cette méthode a connu un développement rapide entre 1960 et 1970 sous l’impulsion de Janine Connes, Pierre Connes et leurs élèves.

Le spectromètre est un interféromètre à deux ondes (par exemple, un interféromètre de Michelson) dont on fait varier la différence de marche depuis zéro jusqu’à une valeur D ^m. Si 煉S / 煉 靖 est la densité spectrale de puissance de la source émise vers l’interféromètre, celui-ci transmet: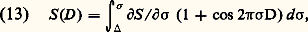

où 靖 est le domaine spectral de sensibilité du détecteur. On reconnaît dans la partie variable avec D la transformée de Fourier en cosinus de la densité spectrale 煉S / 煉 靖 que l’on cherche. Il suffit donc d’effectuer sur l’interférogramme S (D ) la transformation de Fourier inverse pour retrouver l’ensemble des éléments spectraux du spectre étudié:

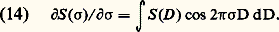Une approximation de cette intégrale est calculée numériquement sur ordinateur à partir de valeurs de S (D ) échantillonnées et numérisées entre D = 0 et D = D ^m. On n’obtient pas exactement 煉S / 煉 靖 mais une image dont la résolution est limitée par la valeur D ^m. La limite de résolution 嗀靖 est égale à 1/D ^m, et le pouvoir de résolution R = 靖 / 嗀靖 = 靖 D^m = D / est égal au nombre de franges N enregistrées dans l’interférogramme.

Le traitement de signal effectué sur ordinateur, multiplication de l’interférogramme par un cosinus suivie d’une intégration sur la durée de l’enregistrement, est équivalent à une détection synchrone de grande sélectivité accordable en fréquence. C’est ce qui justifie le très bon rapport signal sur bruit obtenu par un spectromètre de Fourier sur des modulations interférentielles dont l’amplitude est très inférieure au bruit du détecteur.

L’interféromètre de Michelson utilisé dans la configuration des franges localisées à l’infini (anneaux) présente le même avantage d’étendue que l’interféromètre de Fabry et Perot. L’angle solide admis par l’interféromètre présente la symétrie de révolution, et sa valeur est, comme pour l’interféromètre de Fabry et Perot, simplement liée au pouvoir de résolution théorique par la relation 12.

L’efficacité lumineuse est excellente; elle est donnée par le facteur de visibilité des franges d’interférences au voisinage de la différence de marche nulle. Égal à 1 pour un interféromètre parfait, ce facteur peut pratiquement dépasser 90 p. 100, surtout dans le domaine infrarouge où les longueurs d’onde sont grandes, et les pièces optiques ainsi que les réglages mécaniques peuvent être considérés comme très bons.

Un avantage spécifique de la méthode est le fait que l’interférogramme est enregistré pendant tout le temps de la mesure en superposant sur le détecteur les signaux de tous les éléments spectraux. Cet avantage multiplex conduit à une amélioration du rapport signal sur bruit par rapport à un spectromètre séquentiel à balayage qui doit partager le temps de mesure entre les éléments spectraux étudiés successivement. Cet avantage était essentiel avant l’avènement des détecteurs infrarouges multicanaux, et il reste significatif pour l’étude de spectres moléculaires comportant un très grand nombre d’éléments spectraux.

La démonstration de l’efficacité de la méthode a été faite en 1967 par J. Connes, Pierre Connes et Jean-Pierre Maillard avec les spectres d’absorption des atmosphères planétaires dans le proche infrarouge. Le pouvoir de résolution atteint sur ces objets par les spectromètres à réseaux était de l’ordre de 1 000. Il a été multiplié par 10, puis par 100, atteignant, sur ces objets, le même pouvoir de résolution que celui qui a été obtenu à cette époque avec les spectromètres à réseau sur le Soleil.

Plus démonstratif encore est le calcul du temps nécessaire à un spectromètre classique à réseau et à fentes pour multiplier par 100 son pouvoir de résolution sans perdre en rapport signal sur bruit. Un spectromètre à réseau peut atteindre une telle résolvance, mais le flux qu’il transmet est divisé par 100 à l’entrée du spectromètre, parce que la fente est cent fois plus fine, et il est encore divisé par 100 à la sortie, parce que la source est blanche et que la largeur d’un élément spectral est divisée par cent. Le signal est donc divisé par 10⁴. Le bruit, dans cette mesure, venant essentiellement du détecteur, si l’on suppose que ce bruit est blanc et ne comporte pas de composante anormale de très basses fréquences (bruit de scintillation), il faut intégrer pendant une constante de temps 10⁸ fois plus grande pour retrouver le même rapport signal sur bruit. Comme il y a cent fois plus d’éléments spectraux dans le spectre, le temps total d’enregistrement est donc à multiplier par 10¹⁰. Lorsqu’on sait que la durée d’enregistrement d’un spectre est une nuit, on comprend que ces performances obtenues par la spectrométrie de Fourier étaient totalement hors d’atteinte d’un spectromètre à réseau.

L’obligation de connaître à chaque instant la différence de marche D de l’interféromètre avec une incertitude petite devant la longueur d’onde des radiations étudiées se traduit par une autre qualité de la spectrométrie par transformation de Fourier: la fonction d’appareil expérimentale est très proche de ce que prévoit le calcul de l’intégrale (14); c’est un sinus cardinal si l’interférogramme est brut, une fonction apodisée si on pondère l’interférogramme par des moyens instrumentaux ou numériques. Il en résulte que les fonctions d’appareil pratiques sont très symétriques, et que la mesure des nombres d’ondes dans tout le spectre peut être faite avec une grande exactitude par rapport au moyen de mesure de la différence de marche. Lorsque cette différence de marche est elle-même mesurée par les franges d’interférences données par une radiation monochromatique, le calcul des nombres d’ondes dans le spectre revient à faire une comparaison numérique directe de ces nombres d’ondes avec celui de la radiation de référence. C’est ainsi que Guy Guélachvili a pu comparer, en 1970, les nombres d’ondes du spectre infrarouge de la molécule de gaz carbonique avec les fréquences de résonance électronique de son spectre de radiofréquence, obtenant une des meilleures valeurs de la vitesse de la lumière connue à cette date.

Spectromètres à laser

La spectrométrie instrumentale, comme l’optique instrumentale en général, a beaucoup évolué après l’apparition des lasers. Ce sont d’abord des techniques classiques, comme la spectrométrie Raman ou la fluorescence, qui ont exploité la grande finesse spectrale et la grande densité d’énergie des sources lasers, permettant de joindre un grand pouvoir de résolution spatial à un grand pouvoir de résolution spectral.

La directivité des faisceaux lasers a permis le développement de techniques de contrôle à distance de type Lidar, ou radar optique, grâce auxquelles on peut détecter par résonance, fluorescence ou effet Raman des espèces moléculaires particulières (oxydes d’azote, de soufre).

L’interaction d’atomes et de molécules avec un faisceau laser a conduit les physiciens à des progrès considérables sur la compréhension des structures élémentaires, sur la mesure de paramètres fondamentaux comme la vitesse de la lumière ou la constante de Rydberg. L’interaction d’un jet atomique et d’un faisceau laser à fréquence accordable associée à une détection directe sur le jet ont permis l’étude spectrométrique à très haute résolution sur des atomes très instables produits en très faibles quantités par des accélérateurs de particules. C’est grâce à ces techniques que la raie de résonance du francium, élément radioactif découvert en 1939 par Marguerite Perey, a pu être observée puis analysée en haute résolution, alors qu’elle n’avait pas encore été trouvée en 1978. Les atomes peuvent être ralentis, leur température abaissée jusqu’à quelques microkelvins par des interactions résonnantes adaptées. Les fréquences de résonance de ces atomes peuvent être connues avec une exactitude inconnue jusqu’ici, si bien que la spectrométrie atomique et moléculaire dispose maintenant d’un grand nombre de fréquences de référence connues avec des incertitudes relatives qui peuvent descendre jusqu’à quelque 10 size=1^漣12.

Les techniques lasers associées à des résonances externes ou internes à la cavité Fabry-Perot ont ainsi permis de progresser dans la métrologie des fréquences optiques et dans la connaissance de certaines structures atomiques ou moléculaires. Des applications spectaculaires pourraient en découler dans un avenir proche, comme la détection des ondes gravitationnelles dans le projet franco-italien Virgo ou la détection de compagnons planétaires des étoiles par la mesure très exacte sur un spectre stellaire d’un très faible effet Doppler-Fizeau (quelque 10 size=1^漣10 en valeur relative) sur de grandes périodes (plusieurs années). Des expériences de résonance atomique faites avec des atomes très ralentis (mélasses optiques, fontaine atomique) conduiront, peut-être dans un avenir proche, à une nouvelle définition de la seconde avec des horloges optiques qui, travaillant à fréquence beaucoup plus grande que l’horloge à césium, donneront des exactitudes au moins aussi bonnes dans des durées beaucoup plus courtes.

Ces derniers développements de la spectrométrie instrumentale de très haute résolution, qui marquent l’aboutissement, en cette fin du XX^e siècle, de notre étude de l’atome commencée au XIX^e siècle par Niels Bohr avec le spectre de l’hydrogène, concrétisent et prolongent l’introduction écrite par Alfred Kastler pour cette grande aventure de la connaissance humaine qu’est la physique atomique et moléculaire.

Encyclopédie Universelle. 2012.